This post is all about answering the question: “How deep is the atmosphere?”. The question doesn’t actually have a simple answer, because there is no altitude where the atmosphere suddenly stops and space starts. Instead, the air gets progressively thinner and thinner as you get higher, gradually giving way to the vacuum of space. What can be startling is how quickly the air gets thinner as you travel upwards. On this page I’ll be finding some ways of getting to grips with the scale of the atmosphere.
At the end, I hope that you might agree with me that the atmosphere is really awfully shallow, and that we definitely ought to be looking after it much more carefully than we do at the moment.
What do we mean by “the air gets thinner”?
A cubic metre of air at sea level contains about 1.2 kilograms of air. Higher in the atmosphere, a cubic metre would contain less air. For example, at 9,000 metres (just above the summit of Mount Everest) a cubic metre of air would contain only about 0.47 kilograms of air, less than half as much as at sea level. It is this decrease of mass per unit volume (density) that I mean when I write of the air getting “thinner”.
How high is the top of the atmosphere?
To get a feel for the thickness of the atmosphere, we will look at a number of different definitions of the top of the atmosphere. As well as these, we’ll also look at some altitudes with life-and-death significance. I’ve put any calculations at the bottom of the post.
120 km – the re-entry line
Below an altitude of 120 km, atmospheric effects become noticeable for spacecraft on re-entry.
100 km – the Kármán line
The Kármán line is a common definition of the boundary of space. This beautiful and clever idea rests on two points.
The first point: to be in orbit around the Earth (assuming there’s no atmosphere) there’s a certain speed at which you need to travel. If you travel more slowly than this, you’ll fall out of orbit. At the altitudes we’re talking about, the critical speed is nearly 8 kilometres per second.
The second point: an aeroplane stays up in the air because its wings generate lift as they pass through the air. The thinner the air, the faster the aeroplane must fly in order to generate enough lift to stay airborne. So the higher an aeroplane goes, the faster it must fly to stay up there.
Here’s the clever bit: there comes an altitude where the air is so thin that the aeroplane must travel at about 8 kilometres per second for its wings to generate enough lift to stay up. But at this speed, it’s going fast enough to stay in orbit anyway, even if there were no air and it had no wings.
This altitude, which is about 100 km, is the Kármán line. You could say that it’s where an aeronaut becomes an astronaut.
The picture on the right is a scale diagram showing the Earth (grey) and the atmosphere (blue, thickness defined by the Kármán line). 99.99997% of the atmosphere lies in the blue region.
31 km – the 99% line
99% of the atmosphere is below 31 km above the surface of the Earth. The picture on the right shows roughly what part of central London would look like seen from 31 km. It doesn’t look too far away, but from this altitude, you are looking through nearly the entire atmosphere. (Please note that this picture represents roughly how big things would look from 31 km. It doesn’t reflect the optical degradation that viewing through 31 km of air would produce. I scaled the picture from one taken at an unknown altitude.)
19 km – the Armstrong line
At this altitude the air pressure is lower than the vapour pressure of the water in your body. Uncontained body fluids (such as saliva) would start boiling at this altitude.
About 11km – the pressure-suit line
Above this altitude, a simple oxygen supply is not enough to keep you alive. Aircraft cabins have to be pressurised, or you need to wear a pressure suit.
8 km – top of the constant-density atmosphere
Another way to think about the depth of the atmosphere is to ask “How much air are we looking through when we look upwards through the atmosphere?”. To answer this question, imagine that the air in the Earth’s atmosphere is all at sea-level density, instead of getting thinner and thinner with altitude. With the same total amount of air as in the traditional atmosphere, this imaginary atmosphere will come to an abrupt end at a certain altitude. How deep would this constant-density atmosphere be?
The answer is: a little more than 8 kilometres. Mount Everest would just poke out of the top of it. There are details of the calculation later on.
Looked at in this way, the atmosphere is startlingly shallow. You can commonly look horizontally from one place to another place 9 or more kilometres away. When you are doing this, there is more air between you and the not-very-distant object than there is between you and a star overhead.
5.5 km – the habitation line
It appears that no amount of acclimatisation will enable you to survive indefinitely above an altitude of around 6 km. Lambert (1971) reports that in 1961 a team that spent six months at 5,800 m was less fit at the end of this time than newly-arrived people. He also cites an Andean mine at 5,800 m, where the miners chose to walk up daily from 5,300m rather than live at the higher altitude. The current highest permanent human settlement is La Rinconada, at 5,100 m in the Peruvian Andes.
The photograph on the right shows roughly what Buckingham Palace would look like from 6,000 m altitude. It doesn’t look very far away, but at this altitude you wouldn’t last very long. About 50% of the atmosphere is below the habitation limit.
The habitation line on the map
The photograph on the right shows an ordinary 1:50,000 Ordnance Survey map, familiar to UK hillwalkers. The grid squares visible in the sea are 1 km across. It shows the town of Aberdeen on the Scottish coast. On this scale, the tip of my thumb is at about 6,500 m, comfortably in the region where the air is too thin to support human life for very long. If you were on the north side of Aberdeen, you’d be closer to the uninhabitable zone than you would be to the south side of Aberdeen. Seen this way, the atmosphere seems very shallow. 55% of the atmosphere is below the level of the tip of my thumb.
About 4 km – the oxygen-mask line
Above this altitude, in an unpressurised cabin, an aeroplane pilot is required to use an oxygen supply. Having said that, thousands of people (myself included) climb 4,000-metre peaks in the Alps and nobody uses oxygen.
12 metres – top of the liquid atmosphere
Finally, suppose we condensed the entire atmosphere to its liquid form. How deep would the resulting “ocean” be? The answer: just under 12 metres.
So what?
The alarming thing about the altitudes I’ve listed above is how small they are. Compared to the distances that we regularly travel horizontally across the Earth, these distances are tiny. If you could walk vertically upwards, you’d need an oxygen supply after only an hour. Three hours walking and you’d need a pressure suit. Space itself is only a good day’s bike ride away. If you’re in Birmingham, you’re comfortably closer to space than you are to London.
The tall picture
The tall thin picture on the left at the top of the post is a representation of the way the atmosphere gets thinner with altitude. The density of blue dots is proportional to air density at each altitude, starting with solid blue at sea level. The tick marks on the right-hand side are at 10 km intervals. Note that there is air above 60 km, even though there are no dots. It’s just that the air there is extremely thin, and the dots are so widely spaced that you’d need a much wider picture to have a chance of spotting one.
The picture lets you see at a glance roughly how much of the atmosphere is below any given altitude. The aeroplane silhouette is at a typical cruising altitude for airliners – see how much of the atmosphere is below you when you fly.
You could walk across the bottom of the picture in less than two hours.
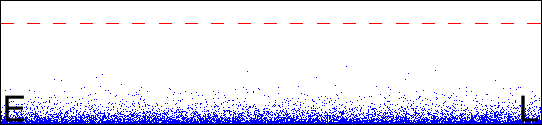
The wide picture
The picture below is drawn on the same principle, but to a different scale. It shows Edinburgh (E), London (L), and the atmosphere. The broken line is the boundary of space as defined by the Kármán line.
Afterthought
You are in the vastness of space. In all directions in front of you, almost empty star-studded space stretches out for unimaginable distances, giving an near- overwhelming feeling of exposure. Behind you is an apparently limitless hard surface. A strange force presses your back firmly against this surface, almost as if it were magnetic. A transparent layer of air, only a few miles thick, between you and the void gives you something to breathe and protects you from the cold of space.
But as on most clear nights, it’s a bit chilly for lying on your back on the ground, so after a while you stand up and walk home to warm your toes in front of the fire.
Details of calculations, and other information
The Kármán line…
…is named after Theodore von Kármán
The 99% line
The pressure at any level in the atmosphere must be exactly that required to support the overlying layers of the atmosphere. The pressure at sea level is enough to support the entire weight of the atmosphere. If the pressure at a given altitude is, say, half sea-level pressure, then we know that half of the mass of the atmosphere must be above this level. Therefore with a table of atmospheric pressures we can quickly work out what fraction of the atmosphere is above any given altitude.
The Armstrong line…
is not named after Neil.
The constant-density atmosphere
Imagine a column of air, of cross-sectional area 1 square metre, that extends through the full height of the atmosphere. The air pressure at the bottom of this column, at sea level, is very close to 105 newtons per metre squared. This means that all of the air in the column of the atmosphere has a weight W close to 105 newtons. The acceleration due to gravity is, for our purposes, constant throughout the height of the column – let’s use g = 9.8 ms-2. The mass of air in the column is given by W divided by g, which comes to 10200 kg. The density of air at sea level is about 1.22 kg m-3, and therefore the volume of air in the column is 10200/1.22 = 8360 cubic metres. As the column has a cross-sectional area of 1 square metre, this means its height is 8360 metres.
The liquid atmosphere
When working out the depth of the constant-density atmosphere, we established that the mass of a column of air of cross-sectional area 1 m2, extending the entire height of the atmosphere, is about 10200 kg. The density of liquid air is about 870 kg m-3, and so if we liquefied this amount of air it would have a volume of 11.7 m3. Hence if we liquefied the atmosphere, the resulting ocean would be 11.7 m deep.
Acknowledgement
This is a minor reworking of a page from my old website. I’m republishing it after receiving an email from Sarah Bush from the Division of Biological Sciences at the University of Missouri, who used the old page as teaching material.
References
Lambert, D. (1971) Medical appendix in Bonington, C. (1971) Annapurna South Face. Cassell.
West, J.B. (2002) Highest Permanent Human Habitation. High Altitude Medicine & Biology, 3, 401-407.