…is broadly similar to the kinetic energy of me and my bike as I pedal along.
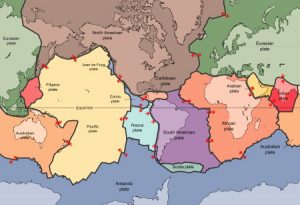
According the the theory of plate tectonics, the outer layer of the Earth is divided into a number of separate plates, which very slowly drift around, opening and closing oceans, causing earthquakes, and thrusting up mountain ranges.
A moving body has energy by virtue of its motion: kinetic energy. Kinetic energy is proportional to a body’s mass and to the square of its speed.
Now tectonic plates move extremely slowly: the usual comparison is with a growing fingernail. But they are also extremely heavy: tens of millions of square kilometres in area, over 100 km thick, and made of rock. I wondered how the minute speed and colossal mass play out against each other: what’s the kinetic energy of a drifting tectonic plate?
There are so many variables, that vary such a lot, that this calculation is going to be extremely approximate. But the answer is delightfully small: the kinetic energy of the tectonic plate on which I live, as observed from one of the plates next door, is about the same as the kinetic energy of me and my bike when I’m going at a reasonable pace: about 1500 joules.

This is a fun calculation to do, but we shouldn’t get carried away thinking about the kinetic energy of tectonic plates. Plates are driven by huge forces, and their motion is resisted by equally large forces. The mechanical work done by and against these forces will dominate a plate’s energy budget in comparison to its kinetic energy.
But the calculation does provoke an interesting thought about forces and motion. I can get my bike up to full speed in, say, 10 seconds. If the Eurasian plate were as free to move as my bike, and I were to put my shoulder against it and shove as hard as I could, it would take me about 500 years to get it up to its (very tiny) full speed.
In both cases, I’m giving the moving object roughly 1500 joules of kinetic energy. How come I can give that energy to my bike in a few seconds, but to give it to the plate would take me centuries?
I’ll return to that thought in a later post.
The calculation
Depending on how you count them, there are 6-7 major tectonic plates, 10 minor plates, and many more microplates. The plates vary hugely in size, from the giant Pacific Plate with an area of 100 million km2, to the dinky New Hebridean plate, which is a hundred times smaller. The microplates are smaller still. Plates also vary a lot in speed: 10-40 mm is typical.
I’m going to be parochial, and choose the Eurasian plate for this calculation.
Let’s call the area of the plate a and its mean thickness t. Its volume is then given by at, and if its mean density is ρ, then its mass m is ρat.
A body of mass m moving at a speed v has kinetic energy ½mv2. So our plate will have kinetic energy ½ρatv2.
The area of the Eurasian plate is 67,800,000 km2 or 6.78 × 1013 m2, and its speed relative to the African plate is (the only speed I have) is given as 7-14 mm per year. We’ll use 10 mm per year, which is 3.2 × 10-10 ms-1. The thickness of tectonic plates in general varies roughly in the range 100-200 km depending upon whether we are talking about oceanic or continental lithosphere; let’s call it 150 km or 1.5× 105 m. The density of lithospheric material varies in the range 2700-2900 kg m-3; we’ll use 2800 kg m-3.
Putting all of these numbers into our formula for kinetic energy, we get a value of 1500 joules (to 2 significant figures, which the precision of the input data certainly doesn’t warrant).
Now for me and my bike. I weigh about 57 kg, my bike is probably about 10 kg. Suppose I’m riding at 15 mph, which is 6.7 ms-1. My kinetic energy is almost exactly…
…1500 joules!
The closeness of these two values is unmitigated luck*, and we shouldn’t be seduced by the coincidence. Just varying the speed of the plate in the range 7-14 mm would cause a 4-fold change in kinetic energy, and there’s the variability in plate thickness and rock density to take into account as well. The choice of bike speed was arbitrary, I guessed the mass of the bike, and I’ve since realised that I didn’t account for the fact that the wheels of my bike rotate as well as translate.
However, what we can say is that the kinetic energy of a drifting continent is definitely on a human scale, which leads to a new question:
Suppose the Eurasian plate were as free to move as my bicycle, and that I put my shoulder against it and shoved, how long would it take me to get it up to speed?
From the figures above, the mass of the plate is 2.85 × 1022 kg. If I can push with a force equal to my own weight (about 560 newtons) then by Newton’s 2nd Law I can give it an acceleration of about 1.96 × 10-20 ms-2. Rearranging the equation of motion v = at, where v is the final speed, a is the acceleration, and t is the time, then t = v/a. Inserting the values for v and a, we get t = 1.6 × 1010 seconds, or about 500 years.
* I didn’t tweak my assumptions: what you see above really is the very first version of the calculation!
Thanks for this very interesting post! The outcome is totally surprising (in terms of my stomach feeling). One would imagine something quantitatively huge for the movement of a continent.
Maybe the more interesting quantity is the momentum then, which is linear in the speed rather than quadratic; thus, the numeric value will be 10 magnitudes bigger.
[Your post hints at the importance of the momentum, which was not much of a topic in my high-school physics education (at least not in the same way as kinetic energy).]
Follow-up question: If you could push the Eurasian plate up to its speed in 500 years ;-), the inertia of the plates cannot serve as an argument for an old Earth…!?
Thanks for your comment, Andreas! The energy-momentum comparison is interesting. If I push very heavy and very light objects for the same time with the same force, the amount of kinetic energy that I give the heavy object is much less than the amount that I give the light object, because work done = force x distance, and the distance through which the force moves is much smaller for the very heavy object. But the amount of momentum that I give each object is equal, because the change of momentum = force x time, and the time involved is the same for both objects. (Could one think of mass as a reluctance to be given kinetic energy?)
Yes, I suppose that if even a single person can get a continent up to speed in 500 years, then in principle we don’t need to postulate an old Earth to account for the current speed of the continents. But I’m inclined to believe in an old Earth anyway 😉
Best wishes
Ben
Could you tell me about how you find the mass of each plate. I saw you said you get it from figures above, but I cannot see that figures. Thank you.
Hi Jangkanipa,
Thanks for your question and sorry for the slow response. The figures you’re after are in the 7th paragraph above the one which refers to the ‘figure above’. The paragraph starts ‘The area of the Eurasian plate…’. I use the area and estimated thickness of the Eurasian plate, and a value for the density of material in the lithosphere.
Ben
This is great – I’ve used your calculations as the basis for a “fun/interesting” university 1st year problem sheet question, many thanks for the inspiration! I was planning to do something simple with volumes and masses but the idea of getting a cyclist to move a plate was just too much fun to leave out 😉
Hi Paul,
I’m delighted that you like my post and have made good use of the idea 🙂 If your students (or you!) come up with any spin-off ideas it’d be great to hear about them.
Cheers
Ben
Hi Ben
Interesting. However, there are a couple of problems.
1) you are dealing with a rigid body rotation (this is the definition of plate tectonics, using Euler’s theorem). The kinetic energy you want to calculate is thus the rotational kinetic energy which is 0.5 * I * omega ^ 2. Omega is the angular velocity vector of the plate, I is the moment of inertia. I is a pig to calculate, and means the equation can only be evaluated numerically. The number that results may not be much different from what you obtained however, since omega is a tiny number of degrees per million years in most cases.
2) The angular velocity needs to be defined relative to a global fixed reference frame independent of plate tectonics. This means something not attached to any moving plate, for instance, markers in the deep mantle. This is difficult stuff. We get large variances in the results for various methods of calculating “absolute” plate motions. A recent paper defined a particular set of deep hot spots in the mantle and fixed plate motions relative to these. The result for Eurasia interestingly, was that it is barely moving at all. This reference frame is probably the most “valid” kinetic reference frame you could derive. The fastest moving plate in this case is the Pacific (omega = 59.79°S, 97.344 E, 0.8023 °/Myr). By contrast, Eurasia has omega = (63.926°N, 6.837°W, 0.0638 °/Myr). Not that the kinetic energy depends not just on the rotation rate, but also the offset of the angular velocity vector from the plate’s centre of mass (because I = sigma (i) (m_i * r_i^2) where each r_i is the distance of some part of the plate of mass m_i to the axis of rotation (omega).
Hi David,
Thanks for your comment and for taking the trouble to discuss the issues in such detail.
1) You are right – I’m guilty, if not of flat-earth assumptions, at least of unspoken flat-earth approximations. To see how much my result is in error, we could view my flat-earth linear calculation as a rotational one by considering the plate to be moving around an Earth-radius cylinder in an exactly circumferential direction at the same omega as the real plate. The use of a cylinder ensures that all parts of the plate are one Earth-radius from the axis of rotation. For a plate that is very thin compared to its distance from the axis of the cylinder, the KE would come out the same whether you considered it as a problem in rotational dynamics or linear dynamics. So my calculated KE will be in error by a factor which is the ratio of the MOI of the imaginary plate on the cylinder to the MOI of the real plate on the Earth with its compound curvature. I’m not sure that the very small value of omega excuses the error: all KEs, no matter how calculated, will scale as omega squared. I see what you mean about the moment of inertia being a pig to calculate; certainly not one for the faint of heart. I’m not even going to try, but my intuition is that my conclusion – that the KE of a drifting continent is laughably small – will remain unscathed. One other (ignored) complication of the spherical case is that the linear speed of the plate is different at different parts of the plate.
2) The lack of a reference frame has nagged at me in a vague sort of way for years. Except for the poles, we have no points of reference. But the using the poles leaves the whole rotational symmetry to deal with. And even the poles wander don’t they? But relative to what? I’ve just read that their wandering is regarded relative to the crust, in which case using them as reference points would be circular. Interesting stuff.
I should also point out, the forces driving plate tectonics are well known and calculated to some degree of accuracy. The plates are mostly subjected to massive gravitational forces due to potential energy gradients. Hence, “ridge push” – the push from oceanic ridges like in the mid-Atlantic – are thought to be of order 2*10^12 Nm-1 . The weird unit that almost looks like what you find on your torque wrench, refers to moment per unit length of ridge (i.e. per metre). You set your torque wrench at maybe 100 Nm for your car wheel bolts. 2*10^12 is 2,000,000,000,000 Nm (per metre of ridge). Ridges are thousands of kilometres long. However, the ridge push force is the small one! The really big one is the pull of the subducting slab wherever these are attached to plates. This force is an order of magnitude greater. The driving forces are so massive because, of course, the resisting forces trying to stop the plates moving are also incomprehensibly big.
I’m a bit puzzled about the units here. You mention the ridge push as being 2*10^12 Nm-1. The units here make sense to me as a force per unit of ridge length. Later on you give the same number but with different units: 2,000,000,000,000 Nm (per metre of ridge). This is (as you say in words) a *moment* per unit length of ridge. Is one of these an error or have I misunderstood?
And if it really is a moment per unit length of ridge, is the moment reckoned about an axis passing through the centre of the Earth? If that’s the case, then the force per unit length of the ridge would be about 300,000 N, which in the general context seems very small.
You mention that the main driving force is the pull of the subducting slab, by an order of magnitude. So is the plate overall under tension? Or at least, is a large part of it under tension? Because of the huge resisting forces on the plate, my intuition is that the plate would be under compression near the ridge, and under tension near the subduction zone, and that there would be a line somewhere between the two where the material was unstressed. Is this somewhere near the truth?